
저번 게시글에서 학습률에 따라 점을 이동한다고 언급했었다.
학습률이 0.01으로 설정되었고 현재 시작점의 기울기가 2.5라고 하면 경사 하강법에서는 둘을 곱한 값인 0.025만큼 다음 지점으로 이동한다. 학습률에 따라 이동하는 크기가 달라지므로 학습률이 작으면 조금씩, 학습률이 크면 큰 보폭으로 점이 이동하게 된다. 한마디로 학습률에 따라 최종 결과값을 얻는 속도에도 영향을 끼친다.
학습률이 클 경우
큰 보폭으로 움직이며 속도가 빠르다.
학습률이 지나치게 클 경우 최종 결과값을 지나칠 수도 있다.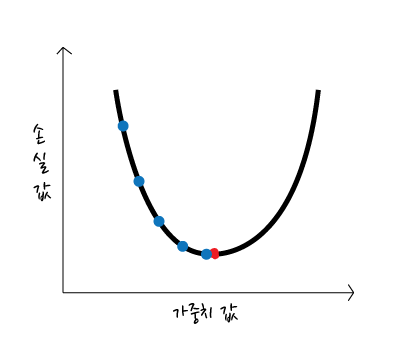
학습률이 작을 경우
작은 보폭으로 움직이며 속도가 느리다.
최종 결과 값에 도달하는 속도가 너무 느려 최종 결과값에 도달하지 못할 수도 있다.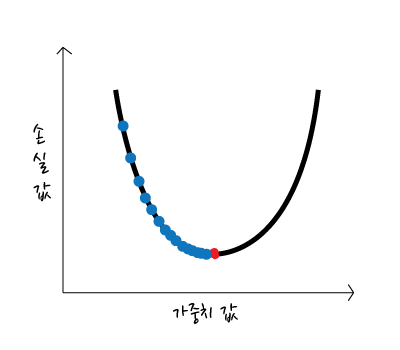
최적의 학습률을 설정한다면 문제가 되지 않겠지만, 최적의 학습률은 어떻게 구할까나..?
골디락스 학습률(Goldilocks learning rate)
이 둘의 사이를 적당히 조절 할 수 있는 방법론 중 하나는 골디락스 학습률을 적용하는 것이다.
만약 같은 학습률로 이동할때 기울기가 크면 기울기가 작은 것보다 더 큰 보폭으로 움직일 것이다.
그래프에서 볼 수 있듯 우측으로 동일하게 움직였지만(빨간 화살표) 실제 움직인 거리는 기울기가 큰 부분이 더 긴 것을 알 수 있다. 따라서 ‘기울기가 작은 부분에서 동일하게 움직이지 않고 좀 더 크게 이동하면 어떨까?’라는 생각에서 나온 것이 골디락스 학습률이다.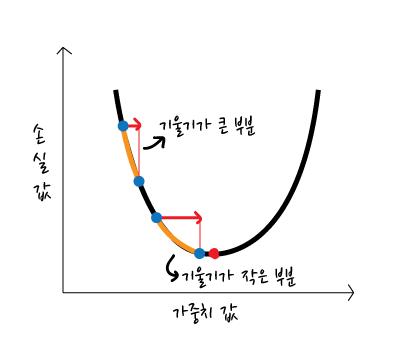
실제 이동한 거리(주황색 선 부분)를 비슷하게 맞춰보았다. 기울기가 작은 부분에서 학습률을 높여 더 큰 보폭으로 이동할 수 있게 하여 속도를 보완할 수 있다.
참고
실무에서는 모델 학습의 성공을 위해 최적 또는 최적에 근접한 학습률을 반드시 구할 필요는 없습니다. 경사하강법이 효과적으로 수렴할 정도로 크지만 발산할 정도로 크지는 않은 적당한 학습률을 구하는 것이 목표입니다.