저번 용어정리에서 회귀는 연속적인 값을 예측하는 것이라고 했다.
넓게 봤을 때 회귀는 기존 데이터를 가지고 새로운 값을 예측하는 것이고,
회귀분석의 종류는 여러가지가 있다. (이 문서에서 다루지는 않겠다)
오늘은 그 중 선형 회귀분석에 대해 알아보려고 한다.
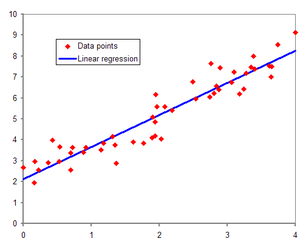
위 그래프에서 빨간 점은 데이터 값이고, 파란색 선은 얻고자 하는 출력, 곧 선형회귀의 결과이다.
선형회귀는 아래와 같은 식으로 나타낼 수 있다.
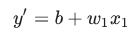
y'는 우리가 얻고자 하는 출력이다. 미분을 했다는 표시로 '(프라임)을 붙인다.b는 편향(y축과 만나는 점)이다. 다른 머신러닝 문서에서 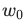
w1은 x1(특성)에 대한 가중치이다.x1은 특성(알려진 입력)이다.
이 공식에서 새로운 결과(y’)를 예측(추론)하고 싶다면 x1에 새로운 값을 넣어보면 된다.
또한, 나중에 다루게 되겠지만 우리는 더 나은 결과를 얻기 위해 가중치를 조절하는 일도 하게 될 것이다.
w1x1은 더 복잡한 모델에서 여러개가 붙어 쓰일 수 있다.
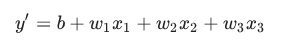
손실

아까 그래프를 다시 보면 파란선과 가까운 빨간점도 있고, 많이 떨어져있는 점들도 볼 수 있다.
점과 선 사이의 거리만큼 우리는 손실이 발생했다라고 말한다.
우리의 목표는 손실이 적은 모델을 만드는 것이다. 즉, 손실은 0에 가까울 수록 좋다.
우리는 모델이 얼마나 정확하게 예측했는가를 알기 위해 손실함수를 쓸 수 있다.
손실함수도 역시 여러 종류가 있지만 이 문서에서는 제곱손실(Squared loss)만 다룬다.
제곱손실
제곱을 하는 이유는 음수(-)의 값이 나왔을 경우에도 양수로 변환할 수 있어 손실률 비교가 쉽고, 손실 값이 발생했을 경우 극대화 시켜 손실된 부분의 패널티를 크게 줌으로써 오차가 더 적은 모델을 만들 수 있기 때문이다.
라벨과 예측 사이의 차이의 제곱
=(observation - prediction(x))^2
= (y - y’)^2
평균제곱오차(Mean Square Error)
한 예시에 평균적으로 오차가 얼마나 발생했는지 알기 위해 쓴다.
각 데이터 별 오차를 합산한 뒤 데이터 갯수로 나눈다.

- (x,y): 예(example)
- x: 모델이 예측하는데 사용하는 특성 집합
- y: 예의 라벨
- prediction(x): 특성 집합(x)과 결합된 가중치 및 편향 함수
- D: (x, y)쌍들의 데이터 세트
- N: D에 포함된 예의 개수
식을 다시한번 해석하자면, (x,y)가 하나의 예고 모든 예를 (y-prediction(x))^2에 대입하여 더한 결과를 1/N하면 평균제곱오차(MSE)가 나온다.